[정리] 시간복잡도

1. O(1) : 입력값에 관계없이 일정하다.  최고차항의 차수가 0

MenOfPassion(A[], n) {
    i = ⌊n / 2⌋;
    return A[i]; # 코드1
}

 

2. O(n) : 입력값에 비례하여 실행시간이 증가한다. 최고차항의 차수가 1

MenOfPassion(A[], n) {
    sum <- 0;
    for i <- 1 to n
        sum <- sum + A[i]; # 코드1
    return sum;
}

• 입력값 n에 따라 반복횟수가 변화한다
• 실행시간이 n의 값에 비례한다.

3. O(n^2) : 입력값 ^ 2에 비례하여 실행시간이 증가한다. 최고차항의 차수가 2

MenOfPassion(A[], n) {
    sum <- 0;
    for i <- 1 to n
        for j <- 1 to n
            sum <- sum + A[i] × A[j]; # 코드1
    return sum;
}

• 입력값 n으로 2번 반복되니 n x n 으로 반복횟수가 n^2이다. 
• 실행시간이 n^2의 값에 비례한다.

3-1

MenOfPassion(A[], n) {
    sum <- 0;
    for i <- 1 to n - 1
        for j <- i + 1 to n
            sum <- sum + A[i] × A[j]; # 코드1
    return sum;
}

• i의 반복횟수 n - 1
• j의 반복횟수 i를 k라 가정하였을 때 n - k

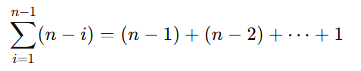
전체 반복횟수를 구하는 공식

• 이 공식은 (n^2 - n )/2 와 동일하다.
• 이때 시간복잡도는 최고차항만을 고려하므로 시간복잡도는 O(n^2)

4. O(n^3) : 입력값 ^ 3 에 비례하여 실행시간이 증가한다. 최고차항의 차수가 3

MenOfPassion(A[], n) {
    sum <- 0;
    for i <- 1 to n
        for j <- 1 to n
            for k <- 1 to n
                sum <- sum + A[i] × A[j] × A[k]; # 코드1
    return sum;
}

• 입력값 n으로 3번 반복되니 n x n x n 으로 반복횟수가 n^3이다.
• 실행시간이 n^3에 비례한다.

4-1

MenOfPassion(A[], n) {
    sum <- 0;
    for i <- 1 to n - 2
        for j <- i + 1 to n - 1
            for k <- j + 1 to n
                sum <- sum + A[i] × A[j] × A[k]; # 코드1
    return sum;
}

• i의 반복횟수 n - 2
• j의 반복횟수 n - i - 1
• k의 반복횟수 n - j
• 전체 반복횟수를 구하는 조합의 수는 n(n-1)(n-2)/6이다.
• 시간복잡도는 최고차항만 고려하므로 시간복잡도는 O(n^3)

 

ex)

O(g(n)) = {f(n) | 모든 n ≥ n0에 대하여 f(n) ≤ c × g(n)인 양의 상수 c와 n0가 존재한다}

함수 f(n) = a1n + a0, 양의 정수 c, n0가 주어질 경우 O(n) 정의를 만족하는지 알아보자.

(출력조건: f(n), c, n0가 O(n) 정의를 만족하면 1, 아니면 0을 출력한다.)

• 모든 n 은 n >= n0 이 성립되어야한다.
• f(n) = a1n + a0 해당함수가 O(n)에 포함되려면 f(n) <= c x n 이 성립되어야 한다.
• a1n + a0 <= c x n 의 식이 성립된다. 여기서 양쪽 모두 a1n을 빼면
• a0 <= c x n - a1n 의 식이 된다.
• a0 <= (c -a1) x n 으로 묶을 수 있다.
• 이러면 c - a1 >= 0 그리고 a0 <= (c - a1) x n의 두가지 조건이 만족해야 한다.

결과적으로 해당 코드가 나타나게 된다.